微分の定義

微分は、これまでに幾度となく登場してきたことからもわかるように、深層学習において最も重要な概念の一つです。 基本的なところから説明していくので、ぜひここでしっかり理解しましょう。

微分するというのは、関数の微分係数あるいは導関数を求めることを指します。これら2つの用語について説明します。

微分係数とは、関数$f(x)$と点$x=a$に対して定義される次の値$f'(a)$です。 なお右辺の極限が収束しないときは$f'(a)$は定義されません。 このとき$f(x)$は点$x=a$微分不可能であるといいます。一方定義されるときは微分可能であるといいます。 以下で関数の微分について述べる際には、その関数が微分可能な点についてのみ考えているとします。 \[ f'(a) =\lim_{h\rightarrow 0} \dfrac{f(a+h) - f(a)}{h} \] 定義としてはこれでいいのですが、この微分係数$f'(a)$の意味合いを考えてみましょう。 右辺の極限の中身についてよく見ると、これは$\dfrac{f(a+h) - f(h)}{(a+h) - a}$と同じです。 この式は、$y=f(x)$のグラフ上で、点$(a, f(a))$と点$(a+h, f(a+h))$を結んだ直線の傾きを表しています。 では、この式において$h\rightarrow 0$とした値にはどんな意味合いがあるでしょうか。 それは、$y=f(x)$の点$(a,f(a))$における接線の傾きになります。 したがって、微分係数を求めることは関数のある点における接線の傾きを求めることに相当します。

続いて導関数について説明します。 これは先ほどの微分係数$f'(a)$をある関数$g(x)$の$x=a$における値$g(a)$とみなしたときの$g(x)$のことで、$f'(x)$や$\dfrac{d}{dx}f(x)$と書きます。 $f'(x)$は次のようにして求められます。 \[ f'(x) = \lim_{h\rightarrow 0} \dfrac{f(x+h) - f(x)}{h} \] 見た目上は、微分係数の式中の$a$を$x$に変えただけですが、微分係数$f'(a)$は単なる値であるのに対し、導関数$f'(x)$は関数であることに注意してください。

さて、$f'(x)$は関数ですから、さらにその導関数を考えることができます。これは$f''(x)$と書きます。 当たり前のことですが、これは以下のように求まります。 \[ f''(x) = \lim_{h\rightarrow 0} \dfrac{f'(x+h) - f'(x)}{h} \] この$f''(x)$の2階導関数といいます。以下同様にして3階導関数、4階導関数などが定義されます。 なお3階以上の導関数については、$f^{(3)}(x)$や$f^{(4)}(x)$などと書くことが多いです。 また導関数$f'(x)$のことを$f(x)$の微分といったり、n階導関数をn次微分ということもあります。

微分の定義がひととおり済んだところで、記法について少し補足しておきます。 先ほど関数$f(x)$の導関数を$f'(x)$と書いていましたが、例えば$y=x^2+1$のように$y$を$x$の関数として表すときには、 $y$の導関数を$y'$あるいは$\dfrac{dy}{dx}$と書きます。 そして2階導関数は$y''$あるいは$\dfrac{dy^2}{d^2x}$と書き（後者の$^2$の位置に注意）、n階導関数を$y^{n}$あるいは$\dfrac{dy^n}{d^nx}$と書きます。 同じものに対していくつかの記法が使われているので混乱するかもしれませんが、場面に応じて使いこなせると便利です。

1変数関数の微分

先ほど微分の定義を学んだので、1変数関数の微分が実際にどうなるかの例を見てみましょう。 1変数関数というのは、値をちょうど1つ受け取る関数のことで、$f(x)$などと表されます。 Lesson 7 で登場したような関数はいずれもこれに当てはまり、また先ほどまでの説明も1変数関数を想定していました。

ではまず1変数関数$y=x$の微分を考えてみましょう。定義に従って計算していくと次のようになります。 \begin{align*} y' &= \lim_{h\rightarrow 0} \dfrac{(x+h)-x}{h} \\ &= \lim_{h\rightarrow 0} \dfrac{h}{h} \\ &= \lim_{h\rightarrow 0} 1 \\ &= 1 \end{align*} よって$y'=1$となります。$y=x$の傾きはどの点においても1なので、この結果には納得がいくと思います。 続いて$y=x^2$の微分を考えてみましょう。 \begin{align*} y' &= \lim_{h\rightarrow 0} \dfrac{(x+h)^2-x^2}{h} \\ &= \lim_{h\rightarrow 0} \dfrac{((x+h)+x)((x+h)-x)}{h} \\ &= \lim_{h\rightarrow 0} \dfrac{(2x+h)h}{h} \\ &= \lim_{h\rightarrow 0} (2x+h) \\ &= 2x \end{align*} よって$y' = 2x$です。 では、$n$を（2以上の）自然数として$y=x^n$の微分を考えてみましょう。 \begin{align*} y' &= \lim_{h\rightarrow 0} \dfrac{(x+h)^n-x^n}{h} \\ &= \lim_{h\rightarrow 0} \dfrac{x^n + {}_nC_1x^{n-1}h+ {}_nC_2x^{n-2}h^2+ \cdots + {}_nC_nh^n - x^n}{h} \\ &= \lim_{h\rightarrow 0} \dfrac{ {}_nC_1x^{n-1}h+ {}_nC_2x^{n-2}h^2+ \cdots + {}_nC_nh^n}{h} \\ &= \lim_{h\rightarrow 0} \dfrac{h({}_nC_1x^{n-1} + {}_nC_2x^{n-2}h + \cdots + {}_nC_nh^{n-1})}{h} \\ &= \lim_{h\rightarrow 0} ({}_nC_1x^{n-1} + {}_nC_2x^{n-2}h + \cdots + {}_nC_nh^{n-1}) \\ &= {}_nC_1x^{n-1} \\ &= nx^{n-1} \end{align*} 以上のことから、任意の自然数$n$に対して$(x^n)'=nx^{n-1}$となることがわかります 実は、任意の実数$\alpha$に対して$(x^\alpha)'=\alpha x^{\alpha-1}$が成り立つことが知られています）。 定数関数についても確認しておきましょう。$c$を定数として、$y=c$の微分は \[ y' = \lim_{h\rightarrow 0} \dfrac{c - c}{h} = 0 \] になります。定数関数は傾きが0の直線と解釈できることとも整合しています。

さて、微分については以下のような性質（線形性）が成り立ちます。

• $(f(x)+g(x))'=f'(x)+g'(x)$
• $(kf(x))'=kf'(x) \quad$ ($k$は定数)

微分の定義にしたがって上記の式の左辺を計算していくと、いずれも右辺に一致することがわかります。 これらのことと先ほどの$x^n$の微分を用いると、多項式の微分が簡単にわかります。例えば$f(x)=2x^3+4x+1$の微分は、 \begin{align*} f'(x) &= (2x^3)' + (4x)' + (1)' \\ &= 3\cdot 2x^2 + 4\cdot 1 + 0 \\ &= 6x^2 + 4 \end{align*} と計算できます。

また次のような公式も成り立ちます（積の微分、商の微分）

\begin{align*} (f(x)g(x))' &= f'(x)g(x) + f(x)g'(x) \\ \left(\dfrac{1}{g(x)}\right)' &= -\dfrac{g'(x)}{(g(x))^2} \\ \left(\dfrac{f(x)}{g(x)}\right)' &= \dfrac{f'(x)g(x)-f(x)g'(x)}{(g(x))^2} \end{align*}

3行目の商の微分については、分子の項の順番に気をつけましょう。

基本的な微分公式

先ほどは微分の性質や多項式関数の微分について学びましたが、覚えておくべき微分公式は他にもいくつかあるので、それらを結果のみ紹介します。 興味のある方は証明にチャレンジしてみたり調べてみたりすると良いでしょう。

合成関数の微分

合成関数$(g\circ f)(x)$を微分することを考えます。これは以下のようになります。 \[ (g\circ f)'(x) = g'(f(x))f'(x) \] これは$u=f(x)$、$y=g(u)$とおいて次のようにも表せます。 \[ \dfrac{dy}{dx} = \dfrac{dy}{du} \cdot \dfrac{du}{dx} \]

合成関数の微分は非常に便利な手法です。 なぜなら、関数を合成して全体として複雑な関数$(g\circ f)(x)$があったとき、直接的にはその微分が求められなくても、 $\dfrac{dy}{du}$と$\dfrac{du}{dx}$、つまり$f'(x)$と$g'(y)$を求めることに問題を「分解」して、それぞれ求めれば合成関数全体の微分がわかるからです。

例として、$y=(3x^2+x+2)^3$の微分を考えてみます。これは$f(x)=3x^2+x+2$、$g(u)=u^3$とおくと合成関数$(g\circ f)(x)$とみなせて、 $f'(x)=6x+1$、$g'(u)=3u^2$であるので、

\begin{align*} y' &= (g\circ f)'(x) \\ &= g'(f(x))f'(x) \\ &= 3(f(x))^2(6x+1) \\ &= 3(3x^2+x+2)^2(6x+1) \end{align*}

となります。

合成関数の微分は、ニューラルネットワークにおける誤差逆伝播法の肝になる部分でもあるので、 公式を覚えるだけでなく実際に使って身に着けていきましょう。

逆関数の微分

関数$f(x)$の逆関数$x=g(y)$の微分を考えます。これは以下のようになります。 \[ \dfrac{dx}{dy} = \dfrac{1}{\dfrac{dy}{dx} } \] これは次のようにもかけます。 \[ g'(y) = \dfrac{1}{f'(x)} = \dfrac{1}{f'(g(y))} \] つまり、逆関数の微分は、元の関数の微分の逆数として得られます。

$x=g(y)$の両辺を微分（合成関数の微分を利用）することで証明できますが、 $y=f(x)$のグラフと$y=g(x)$のグラフが直線$y=x$について線対称になることを考えると逆関数の微分がこのようになることを直観的に理解できると思います。

対数関数の微分

対数関数の微分を考えます。自然対数関数の微分は次のようになります。 \[ (\log x)' = \dfrac{1}{x} \] また一般の対数関数については次のようになります。 \[ (\log_a x)' = \left(\dfrac{\log x}{\log a}\right)' = \dfrac{1}{x \log a} \] 自然対数関数の微分だけ覚えておけば、一般の対数関数の微分も（底の変換公式により）簡単にできることが分かるかと思います。 なお、実は真数に絶対値がついてるときにも同様に微分ができます。 \[ (\log |x|)' = \dfrac{1}{x} \] 真数に絶対値がついていても微分した後には絶対値がつかないことに注意しましょう。

対数関数の微分には1つ重要な応用例があります。それは次に述べる対数微分法です。 今、$y=f(x)$の微分を求めたいとします。 このとき、まず両辺の対数をとります。 なお、対数の真数は正に限るので、$f(x)$が正のときにしか使えないことに注意してください。 先に両辺に絶対値をつけてから対数をとることもできます。 すると$\log y=\log f(x)$（あるいは$\log |y|=\log |f(x)|$）となりますが、これの両辺を微分すると \[ \dfrac{y'}{y} = (\log f(x))' \] となります（左辺では対数関数の微分と合成関数の微分が使われています）。これより \[ y' = y(\log f(x)) = f(x)(\log f(x))' \] となることがわかります。これが対数微分法です。つまり、$f(x)$の微分を求めるには$\log x$の微分がわかればよいということになります。 $f(x)$の微分は求めるのが難しくても、対数の性質のおかげで$\log x$の微分は求めやすいというときに有効です。

いくつかの対数微分法の利用例を見てみましょう。まず$y=f(x)=\dfrac{(x^2+1)^3(x+2)}{(x^3+x+1)^2}$の微分を対数微分法によって求めてみましょう。 次のようになります。

\begin{align*} \log |y| &= \log |f(x)| \\ &= \log \dfrac{|(x^2+1)^3(x+2)|}{|(x^3+x+1)^2|} \\ &= 3\log |x^2+1| + \log |x+2| - 2\log|x^3+x+1| \\ \dfrac{y'}{y} &= 3\cdot \dfrac{2x}{x^2+1} + \dfrac{1}{x+2} - 2\cdot\dfrac{3x^2+1}{x^3+x+1} \\ &= \dfrac{6x}{x^2+1} + \dfrac{1}{x+2} - \dfrac{6x^2+2}{x^3+x+1} \\ y' &= y\left(\dfrac{6x}{x^2+1} + \dfrac{1}{x+2} - \dfrac{6x^2+2}{x^3+x+1}\right) \\ &= \dfrac{(x^2+1)^3(x+2)}{(x^3+x+1)^2}\left(\dfrac{6x}{x^2+1} + \dfrac{1}{x+2} - \dfrac{6x^2+2}{x^3+x+1}\right) \end{align*}

これは商の微分などを用いても求められますが、対数微分法によって非常に簡単な計算で求められることがわかります。 次に$y=x^x(x \gt 0)$の微分を考えてみましょう。次のようになります。

\begin{align*} \log y &= \log x^x \\ &= x\log x \\ \dfrac{y'}{y} &= 1 \cdot \log x + x \cdot \dfrac{1}{x} \\ &= \log x + 1 \\ y' &= y(\log x + 1) \\ &= x^x(\log x + 1) \end{align*}

よって$(x^x)'=x^x(負負log x + 1)$となります。これは他の方法で求めるのは難しいです。

ここで、対数関数の逆関数である指数関数についてもその微分の公式を示しておきます。

\begin{align*} (e^x)' &= e^x \\ (a^x)' &= a^x \log a \end{align*} 上記のように、$e$を底とする指数関数は微分しても元と変わらないという、非常に面白い性質があります。

三角関数の微分

三角関数に関する微分公式をいくつか紹介します。

• $(\sin x)' = \cos x$
• $(\cos x)' = -\sin x$
• $(\tan x)' = \dfrac{1}{\cos ^2 x}$
• $\left(\dfrac{1}{\tan x}\right)' = -\dfrac{1}{\sin ^2 x}$

このように、微分が非常に簡単にできることも三角関数の特徴の1つです。 また上記の式からわかることとして、$\sin x$や$\cos x$はそれぞれ4回微分すると元に戻るという性質があります。

極大・極小

微分の応用例の1つに、関数の極大・極小を求めることがあります。 まず用語の説明をします。 ある点$x=a$の前後で関数$f(x)$が減少から増加に転じるとき、$f(a)$を$f(x)$の極小値といい、$a$のことを$f(x)$が極小値をとる$x$の値などといいます。 下に凸な二次関数の頂点が一つの例になります。 同様に、ある点$x=b$の前後で関数$f(x)$が増加から減少に転じるとき、$f(b)$を$f(b)$の極小値といい、$b$のことを$f(x)$が極小値をとる$x$の値などといいます。 こちらは上に凸な二次関数の頂点が一つの例になります。 また極小値と極大値をまとめて極値といいます。なお極値の個数は関数によります（0個のこともあります）。

ここで、微分の意味について再び考えてみましょう。 微分係数の値とは、接線の傾きとみなすことができるのでした。 接線の傾きは、グラフ上で考えれば、「接点の近くにおいてその関数がどのように変化しているか」を表すことがわかります。 つまり、接線の傾きが正であれば接点の近くで関数は増加しており、負であれば接点の近くで関数は減少している、ということがわかります （また接線の傾きの大きさ（絶対値）によって関数の変化の大きさもわかります）。 したがって、微分（導関数）とは、各点においてその近くで元の関数がどんな変化をしているかという情報を持った関数であるといえます。

このことを踏まえると、微分を考えることで極値を求められそうなことがわかります。 具体的には、微分が負から正に変わる点で極小値、正から負に変わる点で極大値をとることになります。

例を見てみましょう。三次関数$f(x)=x^3+x^2-x+2$の極値を求めます。 これの微分は$f'(x)=3x^2+2x-1=(x+1)(3x-1)$となります。 よって$f'(x)$は$x=-1$において正から負に、$x=-\dfrac{1}{3}$において負から正になります。 微分によって極値を求める際には、以下のような表（増減表）をかくと関数の増減がわかりやすくなって便利です。

$x$	$\cdots$	$-1$	$\cdots$	$\dfrac{1}{3}$	$\cdots$
$f'(x)$	$+$	$0$	$-$	$0$	$+$
$f(x)$	$\nearrow$	$3$（極大）	$\searrow$	$\dfrac{49}{27}$（極小）	$\nearrow$

したがって$f(x)$は点$x=-1$で極大値$3$をとり、点$x=\dfrac{1}{3}$で極小値$\dfrac{49}{27}$をとることがわかりました。 参考のために、以下に$y=f(x)$のグラフを提示しておきます。

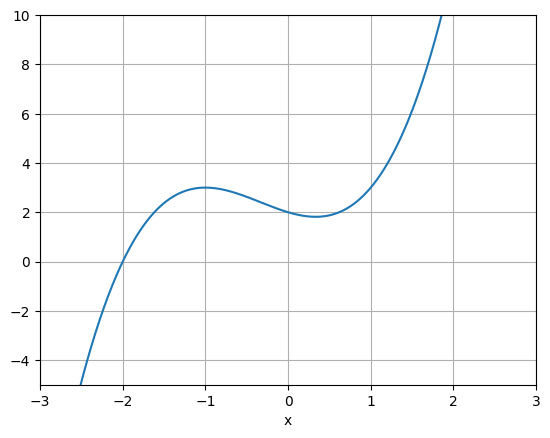$y=x^3+x^2-x+2$のグラフ（Matplotlib により作成）

多変数関数の微分

ここからは多変数関数の微分について考えます。 多変数関数とは、複数の値を受け取る関数のことで、例えば2つの値を受け取るもの（2変数関数）は$f(x,y)$などと書きます。 ここでの多変数関数の説明は、簡単のため2変数関数を用いて行うことにします。 3変数以上の関数でも同様の考え方を使うので、2変数関数についてしっかり理解すれば大丈夫です。

偏微分

これまでは1変数関数の微分を考えてきたので、微分するといったら基本的に$x$について微分することを指していました。 多変数関数では、変数が複数あるので、単に微分というだけではそれがどんな操作を指すのか定かではありません。

多変数関数における微分の1つとして偏微分というものがあります。 これは、ある1つの変数について微分するのですが、その変数以外の変数については定数とみなします。 2変数関数$z=f(x,y)$の偏微分を考えてみます。 変数には$x$および$y$があるので、$x$についての偏微分と$y$についての偏微分が考えられます。 これらをそれぞれ$\dfrac{\partial z}{\partial x}$、$\dfrac{\partial z}{\partial y}$あるいは$f_x$、$f_y$という記号で表します。 1変数関数による微分とは少し記号の違いがあることに注意してください。

先ほど、偏微分では注目している変数以外の変数については定数とみなすという説明をしました。 数学的な厳密な定義は別にあるのですが、実際に偏微分を計算するうえでは上記の説明で十分です。 また、偏微分においても、1変数関数の微分で紹介した線形性や積の微分、商の微分などの公式を使うことができます。

では少し例を見てみましょう。$f(x, y)=2x^2+3xy+2x+4y$の偏微分を考えます。 $x$についての偏微分は次のようになります。 \begin{align*} f_x &= (2x^2)_x + (3xy)_x + (2x)_x + (4y)_x \\ &= 4x + 3y + 2 \end{align*} $x$についての偏微分なので、例えば$4y$などは定数とみなして計算していることに注意してください。 続いて$y$についての偏微分を計算してみます。 \begin{align*} f_y &= (2x^2)_y + (3xy)_y + (2x)_y + (4y)_y \\ &= 3x + 4 \end{align*} 少し偏微分の計算がわかってきたでしょうか。 ではもう一つの例として$g(x,y)=e^{xy}(x + \cos y)$の偏微分を計算してみましょう。 \begin{align*} g_x &= (e^{xy})_x\cdot (x + \cos y) + e^{xy}\cdot(x + \cos y)_x \\ &= ye^{xy}(x + \cos y) + e^{xy}\cdot 1 \\ &= (xy +y\cos y + 1)e^{xy} \\ g_y &= (e^{xy})_y \cdot (x + \cos y) + e^{xy}\cdot (x+\cos y)_y \\ &= xe^{xy}(x+\cos y) + e^{xy}(-\sin y) \\ &= (x^2+x\cos y-\sin y)e^{xy} \end{align*}

偏微分の計算を見てみたところで、偏微分にどんな意味があるかを述べておきます。 偏微分では、注目している変数以外の変数は定数とみなして、つまり固定して考えています。 したがって、偏微分とは、注目している変数のみを動かしたときの関数の増減を表すことになります。

しかし、1変数関数の微分とは異なり、ある値の前後ですべての変数についての偏微分の正負が入れ替わることがわかっても、その点で極値をとるとは限りません。 多変数関数$f(x,y)$では、ある点$(a, b)$の近くのどんな点（点$(a,b)$は除く）$(x, y)$においても$f(a,b)\gt f(x,y)$が 成り立つとき$f(x,y)$は点$(a,b)$で極大値をとるといい、$f(a,b)\lt f(x,y)$が成り立つとき$f(x,y)$は点$(a,b)$で極小値をとるといいます。 このような条件は、偏微分の正負が入れ替わるというだけでは満たされるとは限りません。

すべての変数についての偏微分の正負が入れ替わるにもかかわらず、極値を取らないものの例として、鞍点があります。 これはある方向から見れば極大値だが他のある方向から見ると極小値になっているような点のことです。 例えば$f(x,y)=x^2-y^2$は、原点$(0,0)$において、$x$軸方向について見れば極小値、$y$軸方向について見れば極大値となります（$f_x$および$f_y$を考えればわかります）。 したがって点$(0,0)$は$f(x,y)$の鞍点です。

機械学習では、目的関数を最適化すること、つまり目的関数の極小値をとる点を見つけることが目標です。 しかし、目的関数がパラメータについて複雑になってくると、鞍点を持つことが普通にあります。 このとき、単純な勾配降下法を用いるとパラメータが鞍点にとどまってしまうことがあるので、さまざまな工夫を用いてそれを回避することが行われています。

全微分

多変数関数における微分には、偏微分の他に全微分があります。 2変数関数$f(x,y)$が点$(a,b)$で全微分可能であるとは、十分（絶対値が）小さい$h$、$k$に対し、ある$A$、$B$および$\lim_{(h,k)\rightarrow (0,0)}\varepsilon(h,k)=0$を満たす$\varepsilon(h,k)$が存在して \[ f(a+h, b+k) - f(a, b) = Ah + Bk + \varepsilon(h, k)\sqrt{h^2+k^2} \] となることです。また$f(x,y)$が全微分可能であるとき、 \begin{align*} df &= \dfrac{\partial f}{\partial x}dx + \dfrac{\partial f}{\partial y}dy \\ &= f_xdx+f_ydy \end{align*} と書いて、これを$f$の全微分といいます。

全微分可能の定義はやや複雑に感じるかもしれません。 これは、$z=f(x,y)$のグラフ（3次元空間内）の点$(a,b)$における接平面を考えていることになります。 1変数関数の微分は接線の存在を示していましたが、それと同様の考え方です。 そして全微分の式$ df = \dfrac{\partial f}{\partial x}dx + \dfrac{\partial f}{\partial y}dy$の意味ですが、 これは点$(a,b)$から微小に$(dx,dy)$だけ動かしたとき、$f(x,y)$は $df = \dfrac{\partial f}{\partial x}dx + \dfrac{\partial f}{\partial y}dy$だけ変化するということを表しています。

なお、全微分可能ならば偏微分可能が成り立ちますが、逆は成り立ちません。 よって全微分可能であることは偏微分可能であることよりも強い主張であるということになります。

Chapter 2 では積分について学びます。積分とは、端的に述べると微分の逆の操作のことです。 微積分の中で深層学習において重要なのはChapter1で学んだ微分であり、 それに比べて積分の重要度は劣るといえますが、深層学習におけるさまざまな手法を理解するには積分の知識も必要なので、 最低限の内容をここでは説明します。

不定積分、定積分

積分には大きく分けて2種類あります。不定積分と定積分です。 まずは不定積分です。ある関数$f(x)$に対して、微分して$f(x)$になるような関数全体のことを$f(x)$の不定積分といい、これを次のように表します。 \[ F(x) = \int f(x) dx \] 上記のように、関数$f(x)$や$g(x)$の不定積分を、それぞれ$F(x)$、$G(x)$と書くことが多いです。 また微分して$f(x)$になるような関数を原始関数といいます。 つまり不定積分とは原始関数全体の集合を指します。

続いて定積分です。これは関数$f(x)$と（その定義域内に含まれる）実数$a$と$b$に対して定義されて、以下のように表されます。 \[ \int_a^b f(x) dx = F(b) - F(a) \] ただし$F(x)$は$f(x)$の原始関数です。 これを「$f(x)$を$a$から$b$まで積分する」などといいます。

1変数関数の積分

積分の定義を確認したので、1変数関数の積分の例を見てみましょう（微分と同様、積分も1変数関数を前提として説明していました。 関数$f(x)=x$の不定積分を考えてみます。つまり、微分して$x$になるような関数全体を求めます。 これには、例えば$\dfrac{1}{2}x^2$が考えられるでしょう。これを微分して$x$になることはすぐわかります。 また、他にも$\dfrac{1}{2}x^2+1$や$\dfrac{1}{2}x^2-\dfrac{2}{3}$などもこれに当てはまります。 なぜなら定数を微分しても0になるだけだからです。 このように、原始関数に定数を加えたものもまた原始関数になります。 このことから、積分定数という言葉を使って、不定積分は以下のような形で書かれます。 \[ \int x dx = \dfrac{1}{2}x^2 + C （Cは積分定数） \]

なお不定積分では、以下の性質（線形性）が成り立ちます。

• $\int (f(x) + g(x))dx = \int f(x) dx + \int g(x) dx$
• $\int kf(x) dx = k\int f(x) dx \quad$ （$k$は定数）

それでは次に、定積分を考えてみます。 先ほど述べたように、定積分は原始関数を用いて定義されていますが、原始関数としてどんなものを選んでも定積分の値は変わりません （簡単に理由を述べると、原始関数はお互いに定数の差しかないので、$F(b) - F(a)$という引き算で定数の差は打ち消されてしまうからです）。 よって定積分の計算の際には原始関数は簡単なものを選べばよいということになります。 ここでは$f(x)=x$の原始関数として$F(x)=\dfrac{1}{2}x^2$を選び、$f(x)$を1から2まで積分してみましょう。 \begin{align*} \int_1^2 f(x) dx &= \int_1^2 x dx \\ &= F(2) - F(1) \\ &= \dfrac{1}{2}\cdot 2^2 + \dfrac{1}{2}\cdot 1^2 \\ &= 2 - \dfrac{1}{2} \\ &= \dfrac{3}{2} \end{align*} なお定積分の計算においては$[F(x)]_a^b$という記法がよく使われます。 これは$F(b)-F(a)$のことを指し、次のように使います（原始関数を$F(x)$などと明示的に置かなくても書きやすくなります）。 \begin{align*} \int_1^2 f(x) dx &= \int_1^2 x dx \\ &= \left[\dfrac{1}{2}x^2\right]_1^2 \\ &= \dfrac{1}{2}\cdot 2^2 + \dfrac{1}{2}\cdot 1^2 \\ &= 2 - \dfrac{1}{2} \\ &= \dfrac{3}{2} \end{align*}

定積分にはある重要な意味合いがあります。 それは、$\int_a^b f(x) dx$（ただし$a \leq b$で$a\leq x \leq b$において$f(x)\geq 0$）が、$y=f(x)$のグラフと$x$軸で囲まれた部分のうち$a\leq x \leq b$の部分の面積になることです。 先ほどの例でいえば、直線$y=x$とx軸で囲まれた部分のうち$1\leq x \leq 2$の部分の面積は、$\dfrac{3}{2}$であることになります。 なお、グラフが$x$軸の上にある範囲における積分については面積になりますが、そうでない範囲が積分する範囲（積分区間）に入っているときはそのまま面積にはなりません。 一般には、$a\leq x \leq b$で$f(x)\geq g(x)$となるとき、$\int_a^b (f(x)-g(x)) dx$は、$y=f(x)$のグラフと$y=g(x)$のグラフで囲まれた部分のうち$a\leq x \leq b$の部分の面積になります。 このことを覚えておくと、例えばグラフが$x$軸より下にあるときに、それらで囲まれた部分（の一部）の面積を求めたければ、$-\int_a^b f(x) dx$などとすればよいことがわかります。

以下に定積分の主な性質を並べておきます。

• $\int_a^b (f(x) + g(x))dx = \int_a^b f(x) dx + \int_a^b g(x) dx$
• $\int_a^b kf(x) dx = k\int_a^b f(x) dx \quad$ （$k$は定数）
• $\int_a^b f(x) dx + \int_b^c f(x) dx = \int_a^c f(x) dx$
• $\int_a^b f(x) dx = -\int_b^a f(x) dx$

また、微積分学の基本定理と呼ばれる次のことが成り立ちます。 \[ \dfrac{d}{dx}\int_a^x f(t) dt = f(x) \]

これは微分と積分が逆の操作であることを表している重要な定理です。

基本的な関数の積分

ここでは、いくつかの基本的な関数の積分公式を紹介します。 証明はしませんが、積分は微分の逆なので、これらの公式が成り立つのはすぐに理解できるでしょう。 なお、以下$C$は積分定数とします。

多項式関数の積分

まず定数$c$の不定積分は次のようになります。 \[ \int c dx = cx + C \]

また、$n$を自然数として、$x^n$の不定積分は次のようになります。 \[ \int x^n dx = \dfrac{1}{n+1}x^{n+1}+C \] なお自然数$n$を実数$\alpha (\neq -1)$に置き換えても上記の式は成り立ちます。 べき乗の数が-1のときは次のようになります。 \[ \int \dfrac{1}{x} dx = \log |x| \]

三角関数の積分

主な三角関数の不定積分の公式を紹介します。

• $\displaystyle\int \sin x dx = -\cos x$
• $\displaystyle\int \cos x dx = \sin x$
• $\displaystyle\int \dfrac{1}{\cos ^2x} dx =\tan x$
• $\displaystyle\int \dfrac{1}{\sin ^2x} dx =-\dfrac{1}{\tan x}$

指数関数と対数関数の積分

指数関数および対数関数の不定積分の公式を紹介します。

• $\displaystyle \int e^x dx = e^x + C$
• $\displaystyle \int \log x dx = x\log x - x + C$

置換積分法

積分にはいくつかの手法があります。まず1つ目が置換積分法です。 $f(x)$の積分において、$x=g(t)$と置く（置換する）と、 \[ \int f(x) dx = \int f(g(t)) \dfrac{dx}{dt} dt \] となることがわかります（合成関数の微分によって証明できます）。これを置換積分法といいます。

利用例を見てみましょう。$f(x)=x(2x+1)^4$の定積分を置換積分法によって求めてみます。 $2x+1=t$、すなわち$x=\dfrac{1}{2}(t-1)$と置換すると、$\dfrac{dx}{dt}=\dfrac{1}{2}$であるので、

\begin{align*} \int f(x) dx &= \int x(2x+1)^4 dx \\ &= \int \dfrac{1}{2}(t-1)t^4 \dfrac{dx}{dt} dt \\ &= \int \dfrac{1}{2}(t-1)t^4 \cdot \dfrac{1}{2} dt \\ &= \int \dfrac{1}{4}(t^5 - t^4) dt \\ &= \dfrac{1}{4} \left(\dfrac{1}{6}t^6 - \dfrac{1}{5}t^5\right) + C \\ &= \dfrac{1}{24}(2x+1)^6 - \dfrac{1}{20}(2x+1)^5 + C \\ &= \dfrac{1}{120}(10x-1)(2x+1)^5 + C \end{align*}

となります。

置換積分法は定積分にも利用できます。しかし積分区間を変更することに注意してください。 上の積分を0から1までの定積分に変更したものを計算してみましょう。 このとき$2x+1=t$と置換すると積分区間は$2\cdot 0+1=1$から$2\cdot 1 + 1=3$に変わることに注意すると、 次のようになります。

\begin{align*} \int_0^1 f(x) dx &= \int_0^1 x(2x+1)^4 dx \\ &= \int_1^3 \dfrac{1}{2}(t-1)t^4 \dfrac{dx}{dt} dt \\ &= \int_1^3 \dfrac{1}{2}(t-1)t^4 \cdot \dfrac{1}{2} dt \\ &= \int_1^3 \dfrac{1}{4}(t^5 - t^4) dt \\ &= \dfrac{1}{4} \left[\left(\dfrac{1}{6}t^6 - \dfrac{1}{5}t^5\right)\right]_1^3 \\ &= \dfrac{1}{4} \left(\left(\dfrac{1}{6}\cdot 3^6 - \dfrac{1}{5}\cdot 3^5\right) - \left(\dfrac{1}{6}\cdot 1^6 - \dfrac{1}{5}\cdot 1^5\right)\right) \\ &= \dfrac{1823}{60} \end{align*}

積分区間の変更は忘れがちなので注意しましょう。

部分積分法

積分の手法としては部分積分法もあります。$G(x)$を$g(x)$の原始関数とすると、以下の式が成り立ちます。 \[ \int f(x)g(x) dx = f(x)G(x) - \int f'(x)G(x) dx \] これは積の微分を使うと証明できます。

利用例を見てみましょう。先ほど対数関数の積分を公式として示しましたが、部分積分法によってそれを証明してみます。

\begin{align*} \int \log x &= \int 1\cdot \log x dx \\ &= \int (x)'\log x dx \\ &= x\log x - \int x(\log x)' dx \\ &= x\log x - \int 1 dx \\ &= x\log x - x + C \end{align*}

また定積分の利用例も見てみましょう。$f(x)=x\sin x$を$0$から$\dfrac{\pi}{2}$まで積分してみます。

\begin{align*} \int_0^{\frac{\pi}{2} } f(x) dx &= \int_0^{\frac{\pi}{2} } x\sin x dx \\ &= \int_0^{\frac{\pi}{2} } x(-\cos x)' dx \\ &= [-x\cos x]_0^{\frac{\pi}{2} } - \int_0^{\frac{\pi}{2} } (-\cos x) dx \\ &= \left(\frac{\pi}{2}\cdot\cos \frac{\pi}{2} - 0\cdot \cos 0\right) + \int_0^{\frac{\pi}{2} } \cos x dx \\ &= 0 + \left[\sin x\right]_0^\frac{\pi}{2} \\ &= \sin \dfrac{\pi}{2} - \sin 0 \\ &= 1 \end{align*}

置換積分法と部分積分法を上手に利用することで、さまざまな積分を計算できます。

重積分

重積分とは、多変数関数に関する（定）積分です。ここでは、特に2変数関数に関する多重積分（2重積分）を扱います。

1変数関数における積分区間は、2変数関数では積分領域にあたります。 積分区間は$x$軸上のある区間を指していましたが、積分領域は$xy$平面上のある領域を指します。 2変数関数$f(x,y)$および（その定義域に含まれる）積分領域Dに対して、2重積分は次のように表します。 \[ \iint_D f(x,y) dx dy \]

2重積分の厳密な定義はここではせず、いくつかの計算例を示しておくに留めることにします。 まずは積分領域が長方形である例を見てみましょう。 2変数関数$f(x,y)=x^2(y+1)$を積分領域$D=\{(x,y)|0 \leq x \leq 1, 1 \leq y \leq 3\}$で2重積分します。 積分領域が長方形の場合には、非積分関数をまず$x$について積分（このとき$y$は定数とみなします）した後で$y$について積分すればよいです （先に$y$について積分しても問題ありません）。 したがって以下のようになります。

\begin{align*} \iint_D f(x,y) dx dy &= \iint_D x^2(y+1) dx dy \\ &= \int_1^3 \int_0^1 x^2(y+1) dx dy \\ &= \int_1^3 (y+1) \int_0^1 x^2 dx dy \\ &= \int_1^3 (y+1) \left[\dfrac{1}{3}x^3\right]_0^1 dy \\ &= \int_1^3 (y+1) \cdot \dfrac{1}{3} dy \\ &= \dfrac{1}{3}\left[\dfrac{1}{2}y^2+y \right]_1^3 \\ &= 2 \end{align*}

なお、1変数関数のときは定積分が面積に対応していましたが、2重積分は体積に対応します。 先ほどの例でいうと、3次元空間における$z=f(x,y)=x^2(y+1)$のグラフと$xy$平面で囲まれた部分のうち、積分領域$D$に含まれる部分の体積が2ということになります。

積分領域が長方形でない場合も見てみましょう。 2変数関数$f(x,y)=e^{x+2y}$を積分領域$D=\{(x,y)|1 \leq x \leq 2, x \leq y \leq 2\}$（直角二等辺三角形）で2重積分します。 この場合、$y$の積分区間が$x$で表されているため、先に$y$について積分することになります。

\begin{align*} \iint_D f(x,y) dx dy &= \iint_D e^{x+2y} dx dy \\ &= \int_1^2 \int_x^2 e^{x+2y} dy dx \\ &= \int_1^2 e^x \int_x^2 e^{2y} dy dx \\ &= \int_1^2 e^x \left[\dfrac{1}{2}e^{2y}\right]_x^2 dy dx\\ &= \int_1^2 e^x \cdot \dfrac{1}{2}(e^4-e^x) dx \\ &= \dfrac{1}{2} \int_1^2 (e^{2x}-e^{x+4}) dx \\ &= \dfrac{1}{2} \left[\dfrac{1}{2}e^{2x} - e^{x+4} \right]_1^2 \\ &= \dfrac{1}{2} \left(-e^6+e^5+\dfrac{1}{2}e^4 - \dfrac{1}{2}e^2\right) \\ &= -\dfrac{1}{4}e^2(2e^4 - 2e^3 - e^2 + 1) \end{align*}

なおこのような場合も、積分領域を（意味を変えずに）書き換えることで順番を変えられます。 例えば今回の例でいえば$D'=\{(x,y)|1 \leq x \leq y, 1 \leq y \leq 2\}$として$x$について先に積分しても同じ結果が得られます。 $D$と$D'$が同じ領域を指していることを確かめてください。

極座標変換

多重積分において、直交座標から極座標に変換することで計算が簡単になる場合があります。 （2次元平面上の）極座標とは何かというと、通常の$xy$平面で表された座標$(x, y)$（直交座標）を、次の変換によって写した座標$(r, \theta)$のことです。 \[ \begin{cases} x = r\cos\theta \\ y = r\sin\theta \\ \end{cases} \] $r$は動径、$\theta$は偏角といい、通常$r\geq 0$、$0\leq \theta \lt 2\pi$の範囲を動きます。

多重積分において座標変換を行う際の注意点としては、「座標の変換にともなう項」が必要なことです。 これは1変数関数の置換積分でいうところの$\dfrac{dx}{dt}$にあたります。 「座標の変換にともなう項」は、ヤコビアン$J$と呼ばれ、2次元平面上の極座標変換では次のようになります。

\begin{align*} J &= \begin{vmatrix} \dfrac{\partial x}{\partial r} & \dfrac{\partial x}{\partial \theta} \\ \dfrac{\partial y}{\partial r} & \dfrac{\partial y}{\partial \theta} \\ \end{vmatrix} \\ &= \begin{vmatrix} \cos \theta & -r\sin \theta \\ \sin \theta & r\cos \theta \\ \end{vmatrix} \\ &= \cos\theta \cdot r\cos \theta - (-r\sin \theta) \cdot \sin \theta \\ &= r(\sin^2 \theta + \cos^2 \theta) \\ &= r \end{align*}

ヤコビアンは、上記のように偏微分を並べた行列の行列式として定義されます。 行列については Lesson 9 で学ぶので、今は計算の仕方がわからなくても大丈夫です。 とりあえず、極座標変換におけるヤコビアンの値は$r$になるという結果を覚えておきましょう。

極座標変換は、積分領域に円が含まれるときに有効なことが多いです。 例として、2変数関数$f(x,y)=e^{x^2+y^2}$の積分領域$D=\{(x,y)|x^2+y^2\leq 4\}$（半径2の円）における積分を、極座標変換によって求めてみましょう。 この場合、$r$については$0$から$\sqrt{4}=2$まで、$\theta$については$0$から$2\pi$まで積分すればよく、また$x^2+y^2=r^2$であるので、次のようになります。

\begin{align*} \iint_D f(x,y) dx dy &= \iint_D e^{x^2+y^2} dx dy \\ &= \iint_D e^{r^2} r dr d\theta \\ &= \int_0^2 re^{r^2} \int_0^{2\pi} d\theta dr \\ &= \int_0^2 re^{r^2} \cdot 2\pi dr \\ &= 2\pi \int_0^2 re^{r^2} dr \\ &= 2\pi \int_0^4 re^t \dfrac{dr}{dt} dt \quad (t=r^2) \\ &= 2\pi \int_0^4 re^t \dfrac{1}{\frac{dt}{dr} } dt \\ &= 2\pi \int_0^4 re^t \dfrac{1}{2r} dt \\ &= \pi \int_0^4 e^t dt \\ &= \pi [e^t]_0^4 \\ &= \pi(e^4 - 1) \end{align*}

やや複雑ですが、極座標変換によって2重積分を求めることができました。